Differential Evolutionで大域的最適化

プログラミング

はじめに

Differential Evolutionという手法を使うと、少ないパラメーターで関数の最小化を行うことができます。いわゆる遺伝的アルゴリズムと呼ばれるものです。

アルゴリズム

例としてAckley Functionと呼ばれる関数の最小点を探索してみます。
この関数は(x1, x2)=(0,0)で最小値0を持つので、最小値探索の結果が(0,0)となれば正しく動いていることになります。
Ackley Function

double Ackley(double x1, double x2)
{
  const double n = 2.0;
  const double c = cos(2.0*M_PI*x1) + cos(2.0*M_PI*x2);
  return 20.0 + exp(1.0) - 20.0*exp(-0.2*sqrt(1.0/n*(x1*x1 + x2*x2))) 
                    - exp(1.0/n*c);
}
元ネタ

[1] A comparative study of differential evolution variants for global optimization, 2006.
[2]http://www.cybernet.co.jp/mds/solution/sol3.html

初期状態

パラメーターが存在しそうな範囲[min,max]に対してランダムに点を生成します。
f:id:wildpie:20151003162132p:plain

// // [min, max]でランダムに点を選ぶ
// MatrixXd x(N_, dim_);
// Initialization(x);

void DifferentialEvolution::Initialization(MatrixXd& x)
{
  std::uniform_real_distribution<double> dist(min_, max_);

  x.noalias() = x.unaryExpr([&](double _)  { return dist(rnd_); });

  std::cout << x << std::endl;
  // rowは生成したデータ点、colはパラメーター
  // -0.82978 -4.07661
  //  4.97185 -1.03419
  // ...
}
ランダムに３点選んで１点つくる

さっき生成した点から3点(r1,r2,r3)を選びます。遺伝的アルゴリズムなので、これが親の役割となり、この３点から新たな点を生成します。
f:id:wildpie:20151003163427p:plain
Fは定数で0.5にしています。
これ以外にも、もっと多くの点を使ったり前回よかった点を使うなどの種類があります。

点を混ぜる

３点から作った点vと現在注目している点xを混ぜます。
f:id:wildpie:20151003175849p:plain
CRは定数0.5で、この場合だと50%の確率で新しい点を採用することになります。jrandはパラメーターのインデックスjの乱数で、新しい点uがxとまるっきり同じになることを防ぐ値です。

採用の決定

新しく作った点uがより悪い点、つまり関数値を増やす場合には採用しません。
f:id:wildpie:20151003170655p:plain
以上の処理を繰り返すと収束します。
f:id:wildpie:20151003171031p:plain
f:id:wildpie:20151003171037p:plain

ソースコード
// [0,n)の数列を混ぜる
// n=4で1,0,2,3とか
std::vector<int> DifferentialEvolution::RandPerm(int n)
{
  std::vector<int> r(n);
  std::iota(begin(r), end(r), 0);
  std::shuffle(begin(r), end(r), rnd_);

  return r;
}

void DifferentialEvolution::Mutation(MatrixXd& x)
{
  std::uniform_int_distribution<int> distInt(0, dim_);
  std::uniform_real_distribution<double> distReal(0.0, 1.0);

  for (int i = 0; i < N_; i++) // データ点
  {
    // 3点選ぶ
    std::vector<int> r(RandPerm(N_));
    VectorXd r1 = x.row(r[0]);
    VectorXd r2 = x.row(r[1]);
    VectorXd r3 = x.row(r[2]);

    int jrand = distInt(rnd_);
    VectorXd ui = VectorXd::Zero(dim_);

    for (int j = 0; j < dim_; j++) // パラメータ次元
    {
	double uj = 0.0;
	if (distReal(rnd_) <= CR_ || j == jrand)
	{
	  VectorXd vi = r1 + F_ * (r2 - r3);
	  uj = vi(j);
	}
	else
	{
	  uj = x(i, j);
	}

	ui(j) = uj;
        // 追記：こっちの方がよかった
        //ui(j) = (distReal(rnd_) <= CR_ || j == jrand) 
	//          ? r1(j) + F_ * (r2(j) - r3(j)) 
	//          : x(i, j);
    }

    if (Ackley(ui(0), ui(1)) <=  Ackley(x(i, 0), x(i, 1)))
    {
      x.row(i) = ui;
    }
  }
}

曲線フィッティング

具体例として点が与えられたときに、曲線をフィッティングする問題を考えてみます。だいぶ前にレーベンバーグ・マーカート(Levenberg-Marquardt)法の記事で使った誤差関数を使ってみます。wildpie.hatenablog.com
観測された14点から下式のパラメーターb1, b2を求めることが目的となります。
f:id:wildpie:20151003174855p:plain

// 観測データ
double xa[] = {77.6E0, 114.9E0, 141.1E0, 190.8E0, 239.9E0, 289.0E0, 332.8E0, 378.4E0, 434.8E0, 477.3E0, 536.8E0, 593.1E0, 689.1E0, 760.0E0};
double ya[] = {10.07E0, 14.73E0, 17.94E0, 23.93E0, 29.61E0, 35.18E0, 40.02E0, 44.82E0, 50.76E0, 55.05E0, 61.01E0, 66.40E0, 75.47E0, 81.78E0};

// 誤差関数
double Misra1a(double b1, double b2) 
{
  double sum = 0.0;
  for (int i = 0; i < 14; i++)
  {
    double temp = b1*(1.0 - exp(b2*xa[i])) - ya[i];
    sum += temp*temp;
  }
  return sum;
}

これを実行すると数百回目の試行で238.942, -0.000550157のパラメーターを得ることができました。
微分も使わず力わざで最小値を求めるのも悪くないですね。

Stan Math Libraryでディリクレ分布からサンプルする

プログラミング

はじめに

C++から使うことのできるStan Math Libraryには、統計や機械学習で使う数学の関数が多数実装されています。このライブラリを使って、ディリクレ分布からサンプリングしてみました。

必要なソフト

ちなみにStan Math Libraryはnew BSD licenseです。
コンパイラはVisual Studio 2012を使用したのですが、erf()などが未定義とのエラーになりました。erf()はVisual Studio 2015では標準で対応しているので、今回はVisual Studio 2015を使用しています。
とはいえ、それでもエラーがいくつかでました。double smallの変数名を変えるのと、プリプロセッサに_SCL_SECURE_NO_WARNINGSを追加することで動きます。他にも内部コンパイルエラーとなったり少々あやしいです。

実装

ちょっと前の記事でディリクレ分布からのサンプリングをしました。wildpie.hatenablog.com
これと同じ内容を再現してみます。

プログラムで重要な部分は
stan::math::dirichlet_rng(alpha, engine)です。αを指定するとサンプリング値が返ってきます。結果も前回の記事と同じになりました。

ドキュメントが見当たらないので、何ができるか把握できていませんが使い勝手は良さそうです。
f:id:wildpie:20150725231808p:plain

#include <iostream>
#include <fstream>
#include <random>

#include <Eigen/Core>
using namespace Eigen;

#include <stan/math.hpp>

int main()
{
  VectorXd alpha(3);
  alpha << 8.0, 2.0, 2.0;

  std::default_random_engine engine;
  std::ofstream ofs("result.csv");
  for (int i = 0; i < 10000; i++)
  {
    VectorXd x = stan::math::dirichlet_rng(alpha, engine);
    ofs << x(0) << "," << x(1) << "," << x(2) << std::endl;
  }
  ofs.close();
}

EigenのMatrix function機能

プログラミング

はじめに

EigenにはMatrix functions moduleがあります。これを使うことで、行列のcosやexpを計算することができます。

例(コサイン)

そもそも行列のcosって何でしょう。「matrix function cos」で検索すると、こちらのサイトが見つかりました。
What is the cosine of a matrix? | John D. Cook
このページによると、テイラー展開を行うことで計算をするようです。EigenとMATLABで実装した例を以下に載せます。
f:id:wildpie:20150606184649p:plain
C++

MatrixXd A(2, 2);
A << 1, 2,
	 3, 4;
std::cout << A.cos() << std::endl;
// 結果
//  0.855423 -0.110876
// -0.166315  0.689109

MATLAB

A = [1 2; 3 4]
funm(A, @cos)

I = eye(2);
I - A^2/factorial(2) ...
  + A^4/factorial(4) ...
  - A^6/factorial(6) ...
  + A^8/factorial(8) ...
  - A^10/factorial(10) ...
  + A^12/factorial(12) ...
  - A^14/factorial(14) ...

MATLABの出力

A =
     1     2
     3     4

ans =
    0.8554   -0.1109
   -0.1663    0.6891

ans =
    0.8504   -0.1182
   -0.1773    0.6731

例(exp)

もう一つの例として行列のexpを計算してみます。
f:id:wildpie:20150606191314p:plain
これは現代制御の分野では遷移行列といわれ有名なようです。（MATLAB/Simulinkによる現代制御入門）。せっかくなのでこの本の例題を再現してみます。
現代制御では以下の式で線形システムを表現できます。
f:id:wildpie:20150606193132p:plain
バネとダンパにつながった台車を動かすときの応答を、バネの力など考慮することで、
f:id:wildpie:20150606192816p:plain
と具体化しています。入力u(t)=0、つまりゼロ入力応答は
f:id:wildpie:20150606193340p:plain
より
f:id:wildpie:20150606193520p:plain
と解が求まります。ここで遷移行列が現れました。時刻tから位置y(t)が算出できます。
MATLAB

A = [0 1 
    -10 -2];
C = [1 0];

x0 = [1
    0];
t = 1;
yt = C*expm(A*t)*x0

MATLABの実行結果

yt =
   -0.3469

C++

#include <iostream>
#include <unsupported/Eigen/MatrixFunctions>
using namespace Eigen;

std::complex<double> expfn(std::complex<double> x, int)
{
  return std::exp(x);
}

int main()
{
  const double t = 1.0;
  MatrixXd A(2, 2);
  MatrixXd c(1, 2);
  VectorXd x0(2);

  A << 0, 1, -10, -2;
  c << 1, 0;
  x0 << 1, 0;

  std::cout << c * (A*t).matrixFunction(expfn) * x0;
 // 結果：-0.346893
}

f:id:wildpie:20150606200437p:plain
はじめ1mだけ台車をずらしておいて、手を離すとバネに押されて戻るイメージです。

C++でディリクレ分布からサンプルする

プログラミング

はじめに

最近「続・わかりやすいパターン認識」という本を読んでいます。いわゆるノンパラベイズ本でして、パラメータの事前分布としてディリクレ分布が多用されています。気になったのでC++でサンプリングする方法を調べてみました。

ディリクレ分布のサンプリング

Googleに"dirichlet sampling c++"などと入れてライブラリを探してみると、GNU Scientific Library (GSL)がおすすめと書いてありました。GPLです。
random - Looking for C/C++ implementations of sampling from multinomial and Dirichlet distributions - Computational Science Stack Exchange

他にライブラリを探しても良いのが見つからなかったので困っていましたが、ガンマ分布のサンプルを合計が１になるように正則化すると、ディリクレ分布からのサンプリングと等価となるようです。なぜかは書いてないので分かりませんが、簡単そうなので実装してみます。

sampling - Drawing from Dirichlet distribution - Cross Validated

ガンマ分布

ガンマ分布の実装はC++11標準で対応しています。最初の引数でalphaを指定できます。

std::default_random_engine engine;
std::gamma_distribution<double> gamma(7.5, 1.0);

std::ofstream ofs("result.csv");
for (int i = 0; i < 1000; i++)
{
  ofs << gamma(engine) << std::endl;
}
ofs.close();

f:id:wildpie:20150419173047p:plain

ディリクレ分布

ガンマ分布の値を合計して割ることで生成できます。
三次元で表示するのがむずかしかったので、サンプルした最初の二要素をプロットしています。C++に使いやすい数値計算ライブラリがないのは何でなんでしょうね。SciPyとかR使えば良いんですけど。
f:id:wildpie:20150419181503p:plain

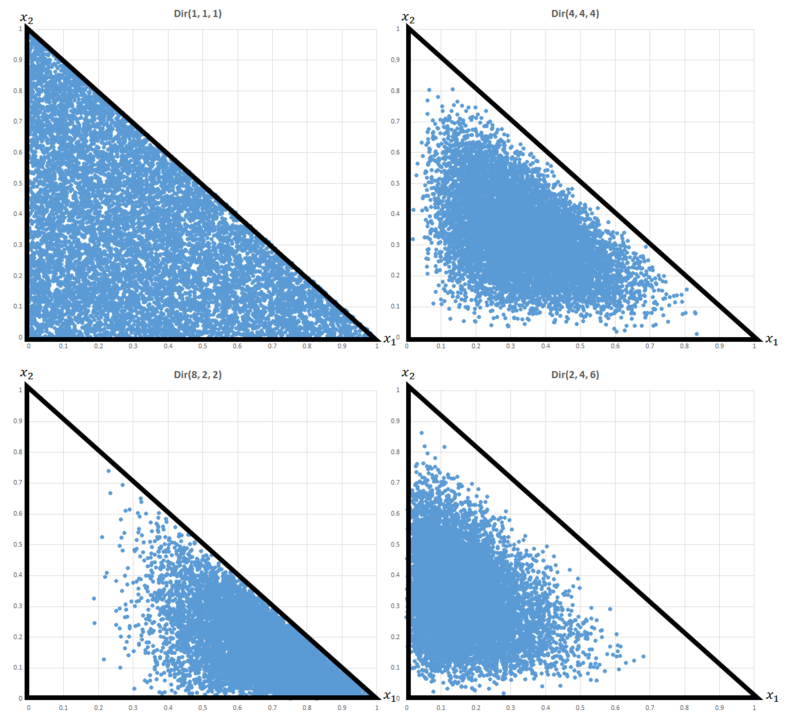
std::default_random_engine engine; // 同じseed
std::gamma_distribution<double> gamma;
VectorXd DirichletSampling(const VectorXd& alpha)
{
  VectorXd x(alpha.size());
  for (int i = 0; i < alpha.size(); i++)
  {
    gamma.param(alpha(i));
    x(i) = gamma(engine);
  }
  x /= x.sum();

  return x;
}

int main()
{
  VectorXd alpha(3);
  alpha << 2.0, 4.0, 6.0;

  std::ofstream ofs("result.csv");
  for (int i = 0; i < 10000; i++)
  {
    VectorXd x = DirichletSampling(alpha);
    ofs << x(0) << "," << x(1) << "," << x(2) << std::endl;
  }
  ofs.close();
}