SVM勉強メモ

プログラミング

SVM

SVM(Support Vector Machine)は2クラスの識別に使えるアルゴリズムで非常に性能が良いらしい。
コンピュータビジョン最先端ガイド2などによるとF(\bf{w})=\sum_{i=1}^n max\{0, 1-y_i \bf{w} ^t \bf {\phi (x_i)}\}+\frac \lambda 2 ||\bf w||^2
を最小化するwを求めるのがSVMとのこと。普通SVMは２次計画法を使って計算するけど、実装方法が分からないので今回はFOBOSを使う。参考１、参考2。
非線形SVMでガウシアンカーネルを使おうとしたけど、カーネルが式に出てこないからカーネルトリックが使えない。何か使う方法があるのかな？
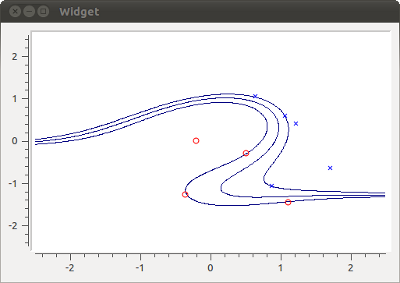
とりあえず多項式カーネル\bf{\phi}: \bf{x}=(x_1,x_2)^t \mapsto (1,\sqrt{3}x_1,\sqrt{3}x_2,\sqrt{3}x_1^2,\sqrt{3}x_2^2,\sqrt{6}x_1 x_2,\sqrt{3}x_1^2 x_2, \sqrt{3}x_1 x_2^2, x_1^3, x_2^3)^tを試す。

実装

多項式

void polynomial(const double x1, const double x2, VectorXd& phi)
{
    phi(0) = 1.0; // w0
    phi(1) = 1.0;
    phi(2) = sqrt(3) * x1;
    phi(3) = sqrt(3) * x2;
    phi(4) = sqrt(3) * x1 * x1;
    phi(5) = sqrt(3) * x2 * x2;
    phi(6) = sqrt(6) * x1 * x2;
    phi(7) = sqrt(3) * x1 * x1 * x2;
    phi(8) = sqrt(3) * x1 * x2 * x2;
    phi(9) = x1 * x1 * x1;
    phi(10) = x2 * x2 * x2;
}

学習の繰り返し

std::vector<double> ori_x;
std::vector<double> ori_y;
std::vector<int> label; // -1 or 1
loadData(ori_x, ori_y, label);

VectorXd w = VectorXd::Zero(11);
for (int a = 0; a < 1000; ++a) // 繰り返し
    for (int i = 0; i < label.size(); ++i) {
        VectorXd phi(11);
        polynomial(ori_x.at(i), ori_y.at(i), phi);
        learn(phi, label.at(i), w);
    }

SVM

void learn(const VectorXd& x, const double y, VectorXd& w)
{
    static double t = 1.0;
    double lambda_0 = 0.01;
    double lambda = lambda_0 / (1.0 + t);
    double eta = 0.01;

    if (y * w.dot(x) < 1.0) {
        w += y * eta * x;
    }

    // L2
    w /= (1.0 + lambda);
    ++t;
}

結果

1と0と-1の線を引いた。
あってる自信は無いのでご注意。