SVM勉強メモ2

プログラミング

LS-SVM

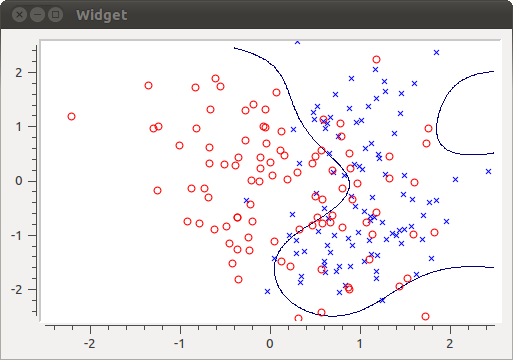
前回、SVMをFOBOSを使って解いた。今回はLeast squares support vector machine(LS-SVM)というSVMの派生アルゴリズムを試してみる。これは最小化問題を
P(\bf{w},b,\bf{\xi})=\frac{1}{2} (w,w)+\frac{C}{2} \sum_{i=1}^n \xi_i^2
s.t.\: y_i-(\bf{w},\bf{\phi}(x_i))+b=\xi\; i=1,...n
としたアルゴリズム。なお、括弧と,は内積を表している。
この式のラグラジアンを微分した結果をまとめると、
\begin{pmatrix} \bf Q & {\bf 1}_n \\ {\bf 1}_n^t & 0 \end{pmatrix} \begin{pmatrix} \bf \alpha \\ b \end{pmatrix}=\begin{pmatrix} \bf y \\ 0 \end{pmatrix}
{\bf Q}_{ij}=k(x_i,x_j)+\frac{1}{C}\delta_{ij}
で表すことができ、出力は以下のようにカーネルを使用する。
f(x)=\sum_{i=1}^n \alpha_i k(x_i,x)+b

実装

ガウシアンカーネル

double kernel_gaussian(const VectorXd& a, 
                       const VectorXd& b, 
                       const double sigma) 
{
    return exp( -(a - b).squaredNorm() / (2.0 * sigma * sigma) );
}

データ準備

std::vector<double> ori_x; // x座標
std::vector<double> ori_y; // y座標
std::vector<double> label; // -1 or 1
loadData(ori_x, ori_y, label); //PRMLのclassification.txt

const int n = label.size();
VectorXd Y(n);
for (int i = 0; i < n; ++i) {
    Y(i) = label.at(i);
}

LS-SVMの計算

double gamma = 100.0; // C
double sigma = 1.5;

MatrixXd K(n, n);
for (int i = 0; i < n; ++i) {
    for (int j = i; j < n; ++j) {
        VectorXd x1(2);
        x1 << ori_x.at(i), ori_y.at(i);
        VectorXd x2(2);
        x2 << ori_x.at(j), ori_y.at(j);
        K(i, j) = kernel_gaussian(x1, x2, sigma);
        K(j, i) = K(i, j);
    }
}

MatrixXd E(n + 1, n + 1);
E << K+(1.0/gamma)*MatrixXd::Identity(n, n), VectorXd::Ones(n),
     VectorXd::Ones(n).transpose(),          0.0;

VectorXd g(n + 1);
g << Y , 0.0;

VectorXd f = E.colPivHouseholderQr().solve(g);
VectorXd alpha = f.head(n);
double b = f.tail(1)(0); // f(n)

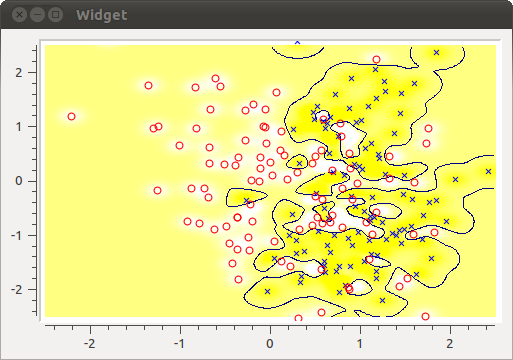
出力値の計算

double value(double _x, double _y)
{
    VectorXd x(2);
    x << _x, _y;

    double sum = 0.0;
    const int n = alpha_.size();
    for (int i = 0; i < n; ++i) {
        VectorXd xi(2);
        xi << ori_x_.at(i), ori_y_.at(i);
        sum += alpha_(i) * kernel_gaussian(xi, x, sigma);
    }

    return sum + b;
}

実行結果が
\sigma=1.5のとき

\sigma=0.1で色を付けたときは

となった。