レーベンバーグ・マーカート法を試す

レーベンバーグ・マーカート法(Levenberg-Marquardt)は非線形の関数最小化ができる手法。誤差関数を最小化することで曲線のあてはめなどができる。

論文を読んでいると最小化はLM法を使用したと一行だけ書いてあることが多い。某学会でなぜLM法を使ったのですかという質問があったけど、みんな使っているからとの回答だった。
前から気になっていたのでどんなもんか試してみる。

ライブラリ

0からプログラムを書くのはしんどいので、ライブラリに頼る。
調べてみたら行列演算ライブラリのEigenに入っていたので、そのまま使う。
グラフの表示にはgnuplot-cpp
http://code.google.com/p/gnuplot-cpp
を使用する。

曲線の当てはめ

Eigenのサンプルを参考にする。
このサイトでデータセットと正解データが公開されているので、正しく最適化されたかどうかが分かる。
http://www.itl.nist.gov/div898/strd/nls/data/misra1a.shtml

例

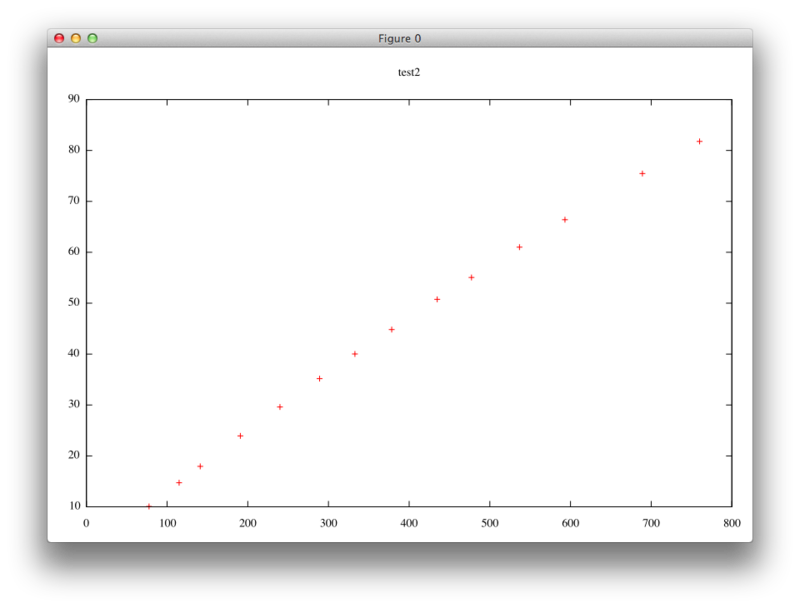
下の図のようにN個の点列が与えられた状態で、
その点を近似する曲線

のを求めることがLM法の目的となる。

最小化したい関数は以下の式で、できるだけ0に近いことが望ましい。

あとLM法は偏微分により最適化を行うため、目的関数の微分をライブラリに教えてあげる必要があるので微分すると


となる。

ソースコードはこんな感じ。

#include <iostream>

#include "Eigen/Dense"
#include "unsupported/Eigen/NonLinearOptimization"
#include "gnuplot_i.hpp"

using namespace Eigen;

struct misra1a_functor
{
    misra1a_functor(int inputs, int values, double *x, double *y) 
    : inputs_(inputs), values_(values), x(x), y(y) {}
    
    double *x;
    double *y;
    // 目的関数
    int operator()(const VectorXd& b, VectorXd& fvec) const
    {
        for (int i = 0; i < values_; ++i) {
            fvec[i] = b[0]*(1.0 - exp(-b[1]*x[i])) - y[i] ;
        }
        return 0;
    }
    // 微分,ヤコビアン
    int df(const VectorXd& b, MatrixXd& fjac)
    {
        for (int i = 0; i < values_; ++i) {
	  fjac(i, 0) = (1.0 - exp(-b[1]*x[i]));
	  fjac(i, 1) = (b[0]*x[i] * exp(-b[1]*x[i]));
        }
        return 0;
    }
    
    const int inputs_;
    const int values_;
    int inputs() const { return inputs_; }
    int values() const { return values_; }
};

int main(int argc, char *argv[])
{
    const int n = 2; // beta1とbeta2で二つ
    int info;
    
    VectorXd p(n); // beta1とbeta2の初期値(適当)
    p << 500.0, 0.0001;
    
    // 入力データ
    double xa[] = {77.6E0, 114.9E0, 141.1E0, 190.8E0, 239.9E0, 289.0E0, 332.8E0, 378.4E0, 434.8E0, 477.3E0, 536.8E0, 593.1E0, 689.1E0, 760.0E0};
    double ya[] = {10.07E0, 14.73E0, 17.94E0, 23.93E0, 29.61E0, 35.18E0, 40.02E0, 44.82E0, 50.76E0, 55.05E0, 61.01E0, 66.40E0, 75.47E0, 81.78E0};

    std::vector<double> x(&xa[0], &xa[14]); // vectorの初期化は不便
    std::vector<double> y(&ya[0], &ya[14]);
    
    misra1a_functor functor(n, x.size(), &x[0], &y[0]);
    LevenbergMarquardt<misra1a_functor> lm(functor);
    info = lm.minimize(p);
    
    std::cout << p[0] << " " << p[1] << std::endl; // 学習結果
    
    Gnuplot g1("test");
    g1.set_title("test");
    g1.set_style("points").plot_xy(x, y); // 点列の描画

    std::stringstream str;
    str << p[0] << "*(1.0-exp(-" << p[1] << "*x))"; 
    
    g1.set_style("lines").plot_equation(str.str()); // 結果の描画
}

結果は以下のようになる。
初期値(500,0.0001)による曲線と最適化後の曲線で、うまいことできている。

数値微分を使う

上の例では関数の微分を指定する必要があった。これだと面倒なので微分はコンピュータにしてもらおう。
NumericalDiff<>というクラスがあるのでこれを使用する。

あんまり大差ないけどソースをのせておく。

#include <iostream>

#include "Eigen/Dense"
#include "unsupported/Eigen/NonLinearOptimization"
#include "unsupported/Eigen/NumericalDiff"
#include "gnuplot_i.hpp"

using namespace Eigen;

// Generic functor
template<typename _Scalar, int NX=Dynamic, int NY=Dynamic>
struct Functor
{
  typedef _Scalar Scalar;
  enum {
    InputsAtCompileTime = NX,
    ValuesAtCompileTime = NY
  };
  typedef Matrix<Scalar,InputsAtCompileTime,1> InputType;
  typedef Matrix<Scalar,ValuesAtCompileTime,1> ValueType;
  typedef Matrix<Scalar,ValuesAtCompileTime,InputsAtCompileTime> JacobianType;
};

struct misra1a_functor : Functor<double>
{
    misra1a_functor(int inputs, int values, double *x, double *y) 
    : inputs_(inputs), values_(values), x(x), y(y) {}
    
    double *x;
    double *y;
    int operator()(const VectorXd& b, VectorXd& fvec) const
    {
        for (int i = 0; i < values_; ++i) {
            fvec[i] = b[0]*(1.0 - exp(-b[1]*x[i])) - y[i] ;
        }
        return 0;
    }
  /*
    int df(const VectorXd& b, MatrixXd& fjac)
    {	
        for (int i = 0; i < values_; ++i) {
	  fjac(i, 0) = (1.0 - exp(-b[1]*x[i]));
	  fjac(i, 1) = (b[0]*x[i] * exp(-b[1]*x[i]));
        }
        return 0;
    }
  */
    const int inputs_;
    const int values_;
    int inputs() const { return inputs_; }
    int values() const { return values_; }
};

int main(int argc, char *argv[])
{
    const int n = 2; // beta1とbeta2で二つ
    int info;
    
    VectorXd p(n); // beta1とbeta2の初期値(適当)
    p << 500.0, 0.0001;
    
    double xa[] = {77.6E0, 114.9E0, 141.1E0, 190.8E0, 239.9E0, 289.0E0, 332.8E0, 378.4E0, 434.8E0, 477.3E0, 536.8E0, 593.1E0, 689.1E0, 760.0E0};
    double ya[] = {10.07E0, 14.73E0, 17.94E0, 23.93E0, 29.61E0, 35.18E0, 40.02E0, 44.82E0, 50.76E0, 55.05E0, 61.01E0, 66.40E0, 75.47E0, 81.78E0};

    std::vector<double> x(&xa[0], &xa[14]); // vectorの初期化は不便
    std::vector<double> y(&ya[0], &ya[14]);
    
    misra1a_functor functor(n, x.size(), &x[0], &y[0]);
    
    NumericalDiff<misra1a_functor> numDiff(functor);
    LevenbergMarquardt<NumericalDiff<misra1a_functor> > lm(numDiff);
    info = lm.minimize(p);
    
    std::cout << p[0] << " " << p[1] << std::endl; // 学習結果
    
    Gnuplot g1("test");
    g1.set_title("test");
    g1.set_style("points").plot_xy(x, y); // 点列の描画

    std::stringstream str;
    str << p[0] << "*(1.0-exp(-" << p[1] << "*x))"; 
    
    g1.set_style("lines").plot_equation(str.str()); // 結果の描画
}

結果が同じなので数値微分でもいいかもしれない。
あと、関数の最小化のやり方がよく分かっていない。
例えばの最小値を求めたいときはどうしたらいいのかな。